Computing fields derived from projected quantities
15 Nov
2010
15 Nov
'10
6:51 p.m.
Howdy folks,
I'd like to calculate the 'lambda' field parameter:
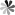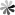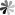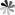
4898
Age (days ago)
4902
Last active (days ago)
1 comments
2 participants
participants (2)
-
 Christopher Moody
Christopher Moody -
 Matthew Turk
Matthew Turk